插入排序

发表于 | 更新于 | 分类于

本篇介绍插入排序排序算法

直接插入排序

直接插入排序（Straight Insertion Sort）：是一种最简单的排序方法，其基本操作是将一条记录插入到已排好序的有序表中，从而得到一个新的，记录数量为1的有序表。

算法步骤
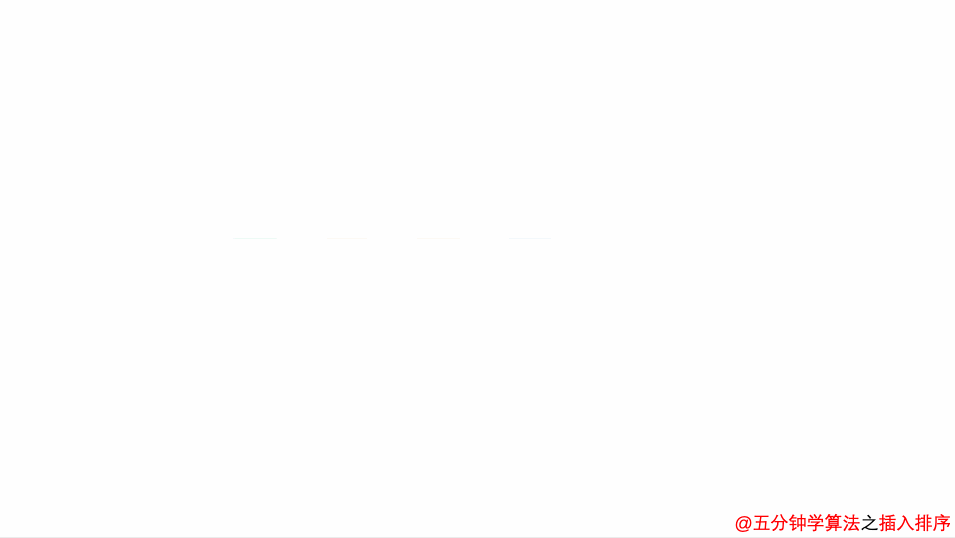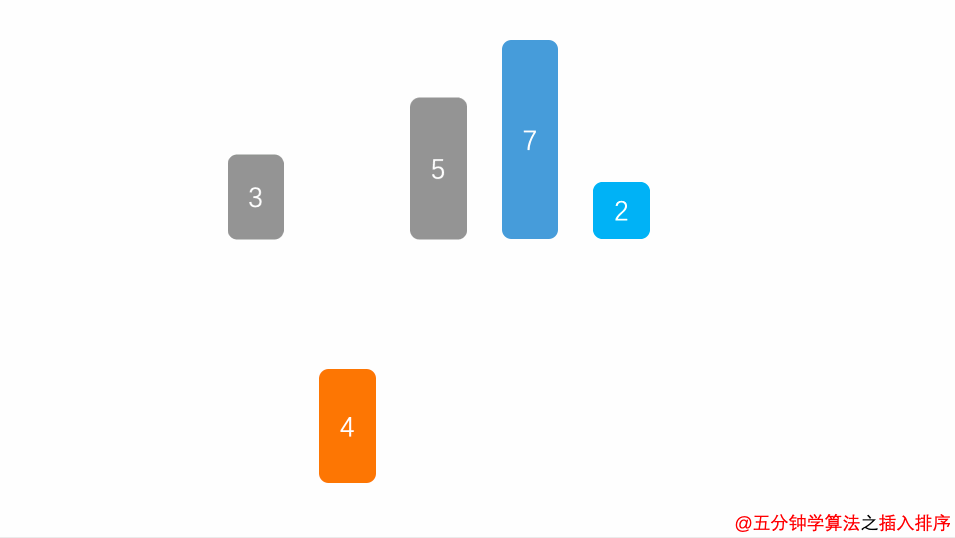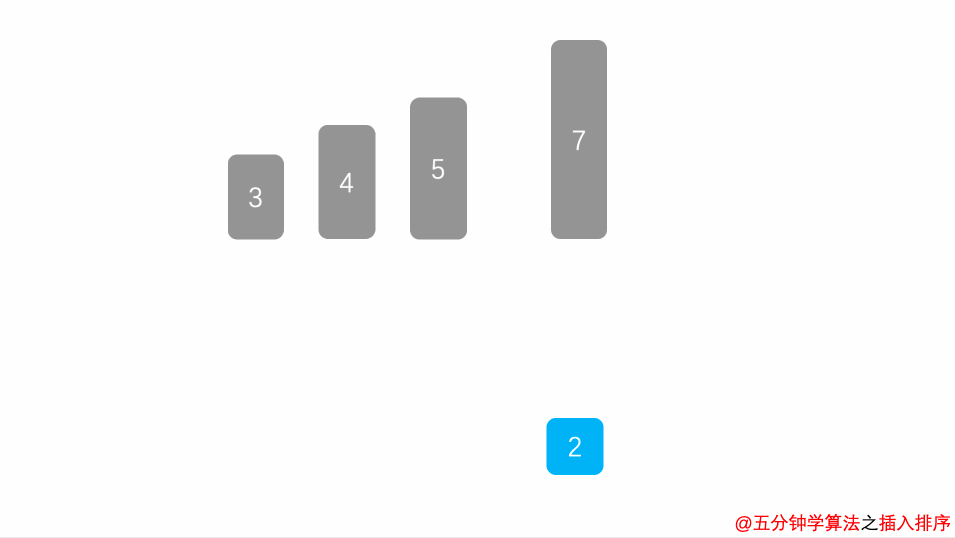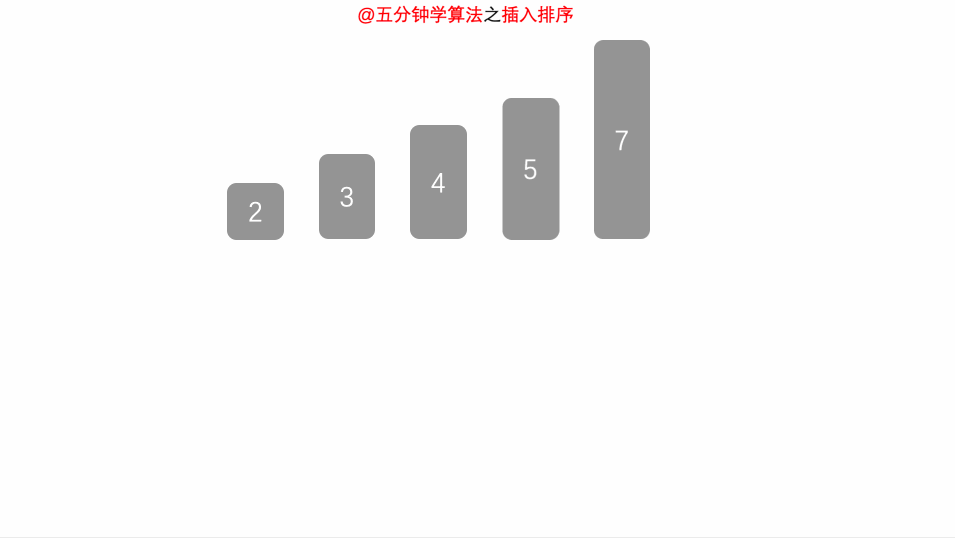
  • 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  • 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
动画演示

图片来源：https://mp.weixin.qq.com/s/vn3KiV-ez79FmbZ36SX9lg

插入排序

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class InsertSort {
    public static void insertSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 1; i < arr.length; i++) {
            for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
                swap(arr, j, j + 1);
            }
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

折半插入排序

折半插入排序（Binary Insertion Sort）：直接插入排序采用查找法查找当前记录在已排好序的序列中的插入位置，这个“查找”操作可利用“折半查找”来实现，由此进行的插入排序称之为折半插入排序。

算法步骤
  • 将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  • 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置，在查找元素的适当位置时，采用了折半查找方法。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class BinsertSort {
    public static void binsertSort(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        for (int i = 1; i < arr.length; i++) {
            int low = 0, high = i-1, tmp = arr[i];
            while(low <= high){
                int mid = (low + high) / 2;
                if(arr[mid] > tmp){
                    high = mid - 1;
                }else{
                    low = mid + 1;
                }
            }
            for(int j = i -1; j >= high + 1; j--){
                arr[j + 1] = arr[j];
            }
            arr[high+1] = tmp;
        }
    }
    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}
算法分析

  1. 时间复杂度

    在平均情况下，折半插入排序仅减少了关键字间的比较次数，而记录的移动次数不变。因此折半插入排序的时间复杂度仍未$O(n^2)$。

  2. 空间复杂度

    只需要一个记录辅助空间，所以空间复杂度为$O(1)$。

  3. 算法特点

    1. 稳定排序
    2. 因为要进行折半查找，所以只能用于顺序结构，不能用于链式结构。
    3. 适合初始记录无序、n较大时的情况。

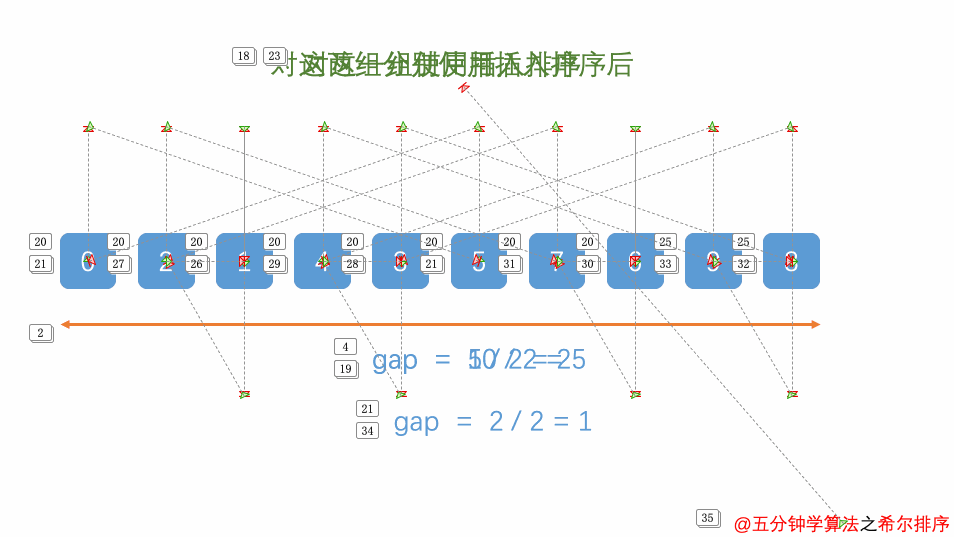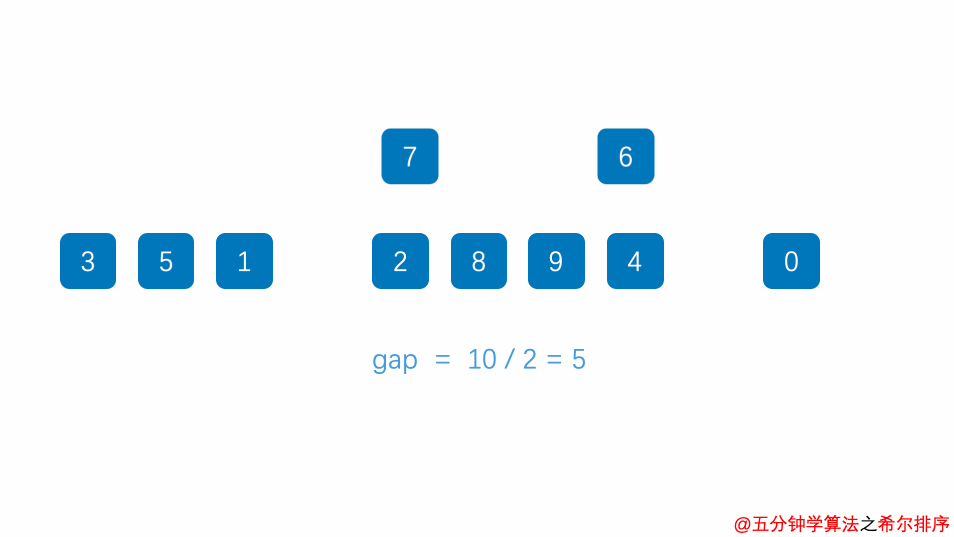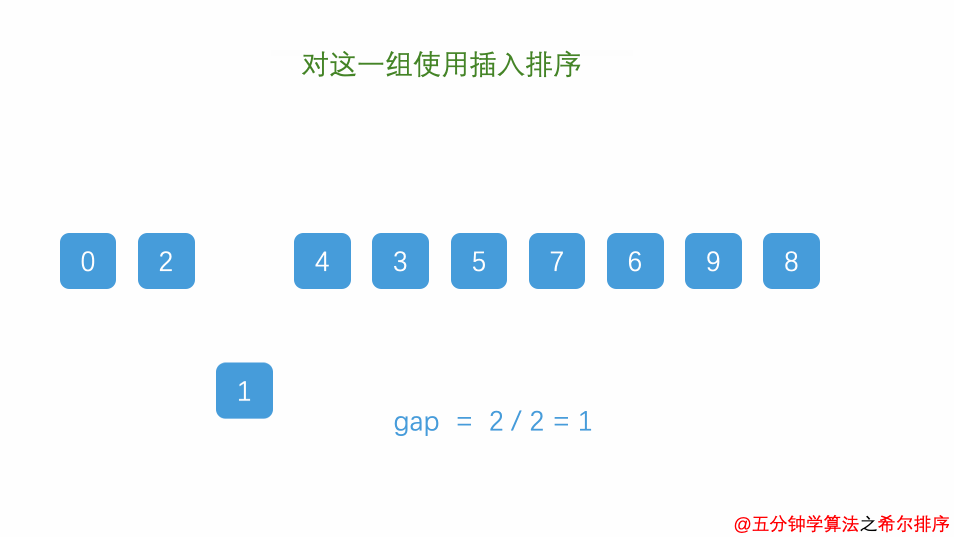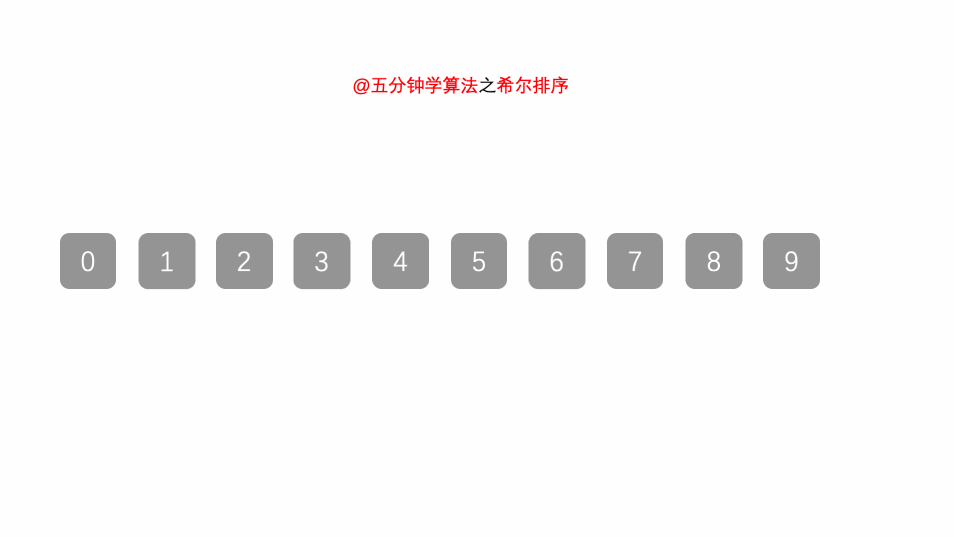
希尔排序

希尔排序：（Shell’s Sort）:又称“缩小量排序”（Diminishing Increment Sort），是插入排序的一种。

算法步骤
  • 选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
  • 按增量序列个数 k，对序列进行 k 趟排序；
  • 每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。
动画演示

图片来源：https://mp.weixin.qq.com/s/vn3KiV-ez79FmbZ36SX9lg

希尔排序

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class ShellSort {
    public static void shellSort(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        for(int gap = arr.length >> 1; gap > 0; gap >>= 1){
            //从第gap个元素，逐个对其所在组进行直接插入排序操作
            for(int i = gap; i< arr.length; i++){
                int j = i;
                while(j-gap >= 0 && arr[j] < arr[j-gap]){
                    swap(arr, j, j-gap);
                    j -= gap;
                }
            }

        }
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}
算法分析

  1. 时间复杂度

    希尔排序中对于增量序列的选择十分重要，直接影响到希尔排序的性能。我们上面选择的增量序列${n/2,(n/2)/2…1}$(希尔增量)，其最坏时间复杂度依然为$O(n^2)$，一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为$O(n^{2/3})$

  2. 空间复杂度

    只有在两个记录交换时需要一个辅助空间，所以空间复杂度为$O(1)$。

  3. 算法特点

    1. 记录跳跃式地移动导致排序方法是不稳定的。
    2. 只能用于顺序结构，不能用于链式结构。
    3. 记录总的比较次数和移动次数都比直接插入排序要少，n越大时，效果越明显。所以适合初始记录无序、n较大时的情况。
0%